Le principe fractal scientifique

ggggggggggggggggggggggggggg

Le terme «fractale» a été inventé par Mandelbrot pour désigner un type d’objets dont l’irrégularité les distingue des figures géométriques euclidiennes telles que la droite ou le cercle. En géométrie euclidienne, les figures ont une dimension entière : 0 pour un point, 1 pour une courbe, 2 pour une surface et 3 pour un volume. En revanche, la dimension d’une fractale peut prendre des valeurs qui ne sont pas des nombres entiers : la dimension fractale constitue une généralisation de la notion de dimension utilisée en géométrie euclidienne.

Les fractales à homothétie interne ont en outre une propriété particulière : chacune de leurs parties reproduit leur totalité. Elles présentent ainsi un aspect tout à fait identique quelle que soit l’échelle considérée : on parle également d’invariance par dilatation. La génération des fractales à homothétie interne est souvent basée sur un algorithme simple. La courbe de Koch, dite «flocon de neige», en constitue un exemple. Ainsi, si l’on examine un flocon de neige naturel à différentes échelles, on observe une structure à peu près identique. On construit la courbe de Koch en reproduisant un triangle équilatéral à des échelles de plus en plus petites. En répétant ce processus une infinité de fois, la courbe obtenue possède alors un périmètre infini mais une aire limitée. Cette propriété se traduit par une dimension fractale strictement comprise entre 1 et 2.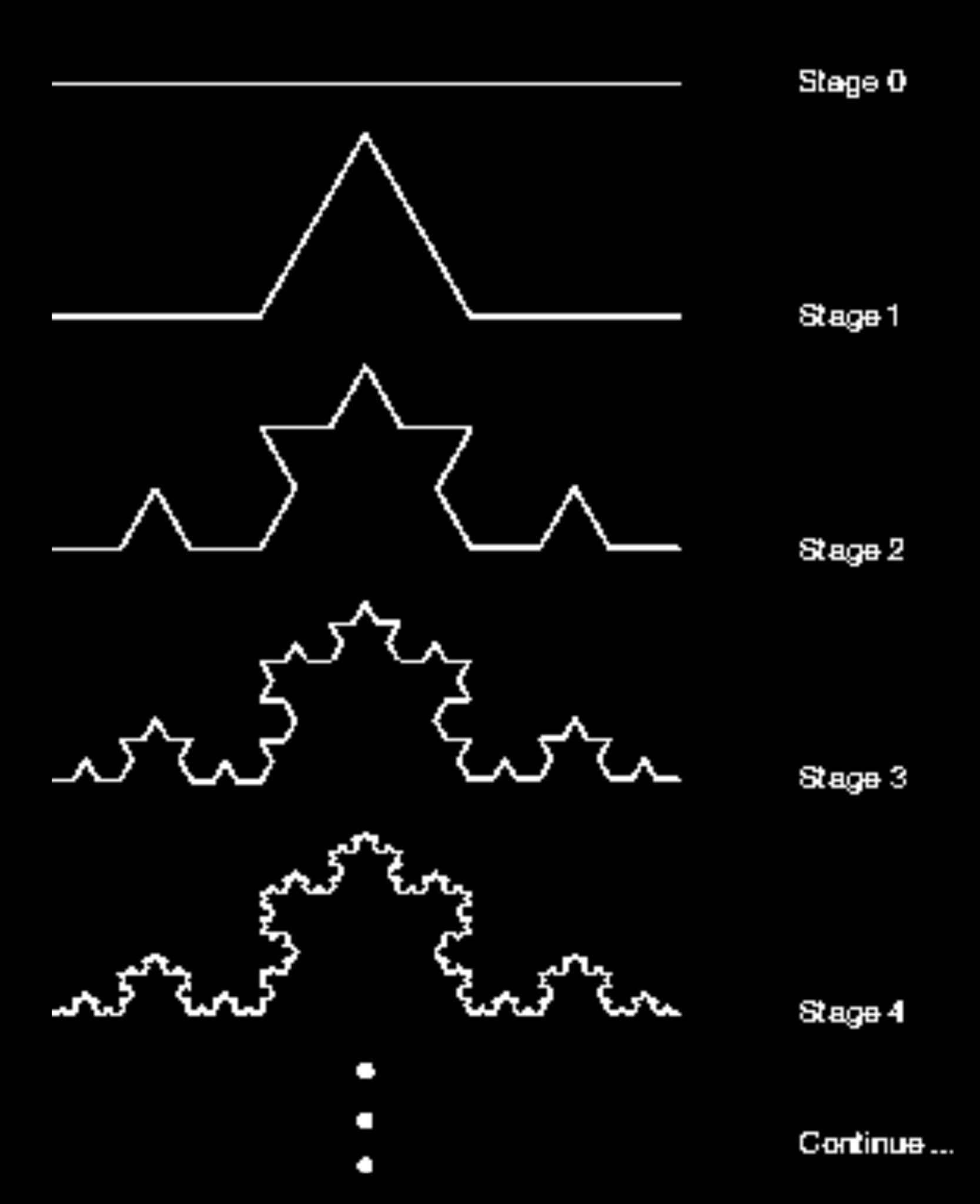

Si l'on considère la courbe de Von Koch, il est aisé de trouver la formule de récurrence qui la génère : en effet, cette courbe est représentative d'une suite géométrique de raison 4/3.

Sur le schéma, on voit distinctement que l'étape 0 (de départ) n'est qu'un segment. On lui donne pour longueur 1n (unité arbitraire). L'étape 1 sera de longueur

1.(4/3) = 4/3n

Soit environ 1,33n, c'est-à-dire 0,33n de plus que l'étape 0. Ainsi, la longueur de la courbe à l'étape 2 sera

(4/3).(4/3) = 16/9n (soit environ 1,8n)

étape 3 : (16/9).(4/3) = 64/27n (soit environ 2,37n)
étape 4 : (64/27).(4/3) = 256/81n (soit environ 3,16n)
...

La longueur de cette courbe va donc en augmentant sensiblement.

Cependant, les ensembles de Julia, tous regroupés dans l'ensemble M de Mandelbrot, permettent de distinguer les limites des fractales : ceci prouve donc que si la longueur d'une fractale tend vers l'infini, sa structure générale peut être contenue dans un plan (ou un espace) et possède une limite finie, puisqu'une fractale est définie par une suite géométrique tendant vers une limite.