ggggggggggggggggggggggggggg
II - Les fractales et la nature
III - Les fractales dans l'Art
1) Les fractales et l'architecture
2) Les fractales dans les arts graphiques
3) Les fractales et la musique
XXème siècle : le changement
Les fractales deviennent un objet mathématique
Apparues au XIXème siècle, les fractales sont considérées comme des curiosités mathématiques jusqu’au milieu du XXème siècle.
Tout comme les plus anciens des théorèmes mathématiques, la théorie fractale comporte un "grand découvreur" : Benoît Mandelbrot fut en effet le premier à considérer les curiosités qu'étaient alors les courbes de Von Koch, de Cantor et de Peano comme des éléments d'une véritable théorie mathématique qui restait à édifier.
Pour l'anecdote, les deux aspects qui inspirèrent à Mandelbrot la possibilité d'un principe mathématique générant les courbes de la nature furent d'une part l'économie et de l'autre la côte bretonne. En effet, avant de s'intéresser rigoureusement aux mathématiques, Mandelbrot s'était spécialisé en économie et avait découvert le mouvement brownien, qui permettait d'établir sinon de prévoir les fluctuations boursières. Ce sont les courbes de la Bourse qui lui évoquèrent la question suivante, parue dans une revue scientifique dans les années 1900 : "Comment calculer la longueur de la côte bretonne ?"
Lorsqu'en 1945 Mandelbrot se tourne vers les travaux de Gaston Julia, il ignore encore qu'il les dépassera : en effet, Julia était un précurseur de la théorie fractale et avait défini des ensembles (qui portent aujourd'hui son nom) destinés d'une part à illustrer tous les types de fractales pouvant exister, et de l'autre à prouver que contrairement à l'impression que l'on pouvait avoir au premier abord, les fractales tendent bien vers une limite dans laquelle elles sont contenues, et non pas vers l'infini.
Benoît Mandelbrot s'intéressa à ces théories et créa l'ensemble M ou ensemble de Mandelbrot, visible ci-dessous :
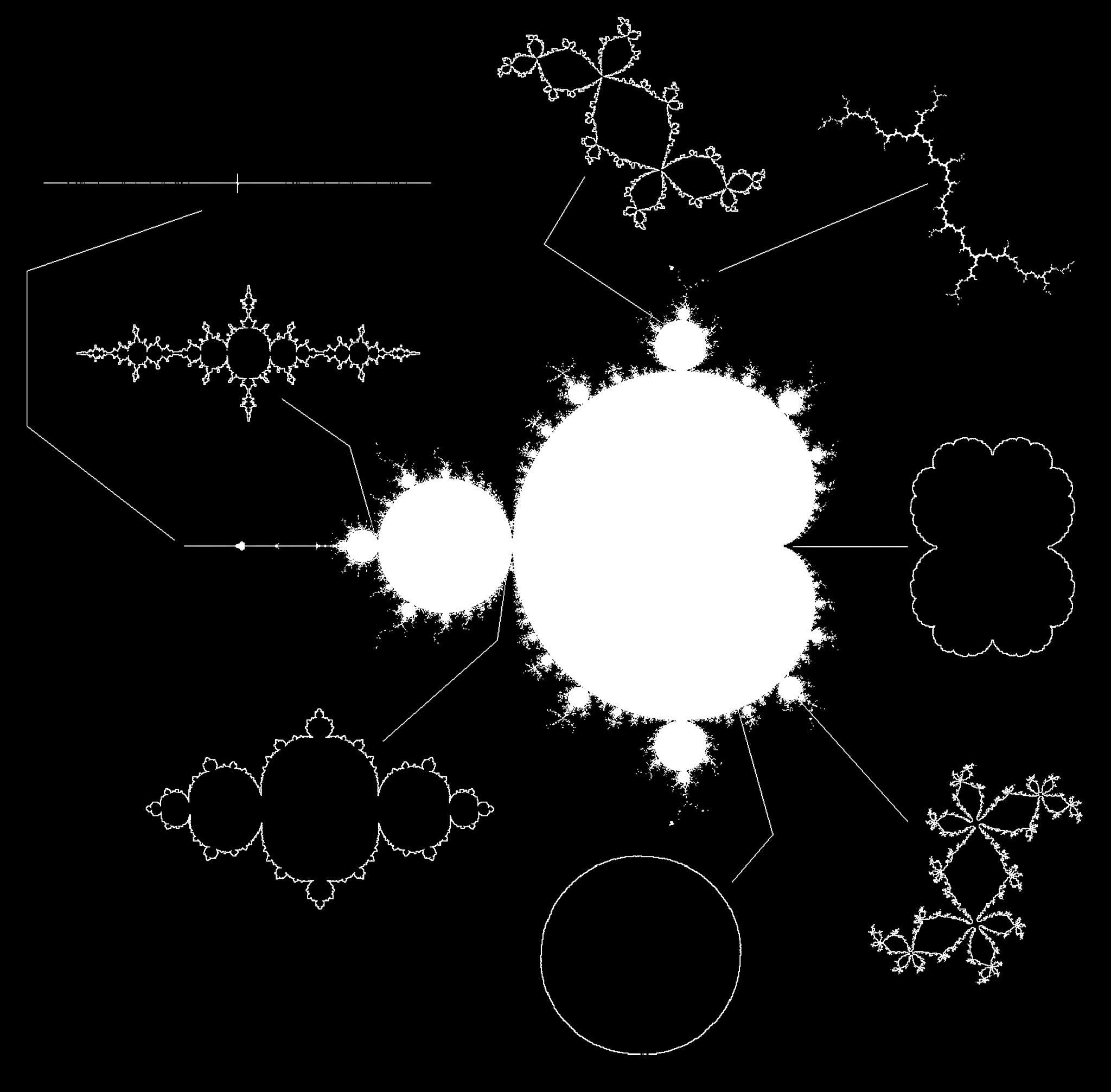
Cet ensemble présente l'intérêt de contenir à lui seul tous les "sous-ensembles" de Julia, comme le montre ce dessin : en zoomant sur chacune des parties de cet ensemble (ainsi que le permet ce lien), on découvre l'un des ensembles de Julia, comme par exemple les quelques exemples qui entourent ici l'ensemble de Mandelbrot.
Mais le principal mérite de Mandelbrot fut d'établir un parallèle entre ses recherches et la Nature, ainsi que personne n'avait songé à le faire auparavant. Il prouva que, contrairement à ce qu'ils croyaient, les géomètres ne s'étaient en rien éloignés de la Nature et de son système de construction en construisant des fractales, mais s'en étaient au contraire bien plus rapprochés que tous les biologistes qui étudiaient alors la question !
Ainsi créa-t-il le mot "fractal" en 1975, (provenant du latin fractus, "irrégulier" ou "brisé").
Aujourd'hui, la théorie fractale a pris de l'essor et a gagné de très nombreux adeptes, mais aussi des opposants : parmi eux, on distingue les pseudo-savants qui, terrifiés par la notion de fractales, voient en elles une forme d'absolue perfection interdite à l'homme, mais aussi les adeptes d'autres théories, filles de la théorie fractale, mais développées selon d'autres paramètres et dans d'autres directions, comme par exemple la théorie constructale.