ggggggggggggggggggggggggggg
II - Les fractales et la nature
III - Les fractales dans l'Art
1) Les fractales et l'architecture
2) Les fractales dans les arts graphiques
3) Les fractales et la musique
Le principe fractal vulgarisé
Si l'on recherche une définition type de "fractales", dans une encyclopédie par exemple, on trouvera :
fractales : figures géométriques de structure complexe dont la création ou la forme met en jeu des règles utilisant le fractionnement. Les fractales sont à la base d’un nouveau système de géométrie permettant de représenter des objets très irréguliers tels que les reliefs montagneux, les amas galactiques ou les côtes rocheuses très découpées.
Encarta, 2001
Il convient de préciser cependant que les fractales ont plusieurs propriétés importantes, qui font d'elles des outils générateurs de paysages idéaux comme expliqué ci-dessus.
Tout
d'abord, dans une fractale, "chaque partie est une miniature du tout".
Ainsi, en zoomant sur une fractale, on obtient exactement la même figure qu'au
départ :
Le périmètre d'une fractale est donc infini, mais l'ensemble de la fractale en elle-même a une limite, puisque le principe fractal consiste à ajouter à l'objet des parcelles de plus en plus petites. Dans le cas de la courbe de Von Koch (animation ci-dessus) on part d'un segment, et par une opération répétée appelée formule d'itération, on obtient une figure dont la longueur tend vers l'infini :
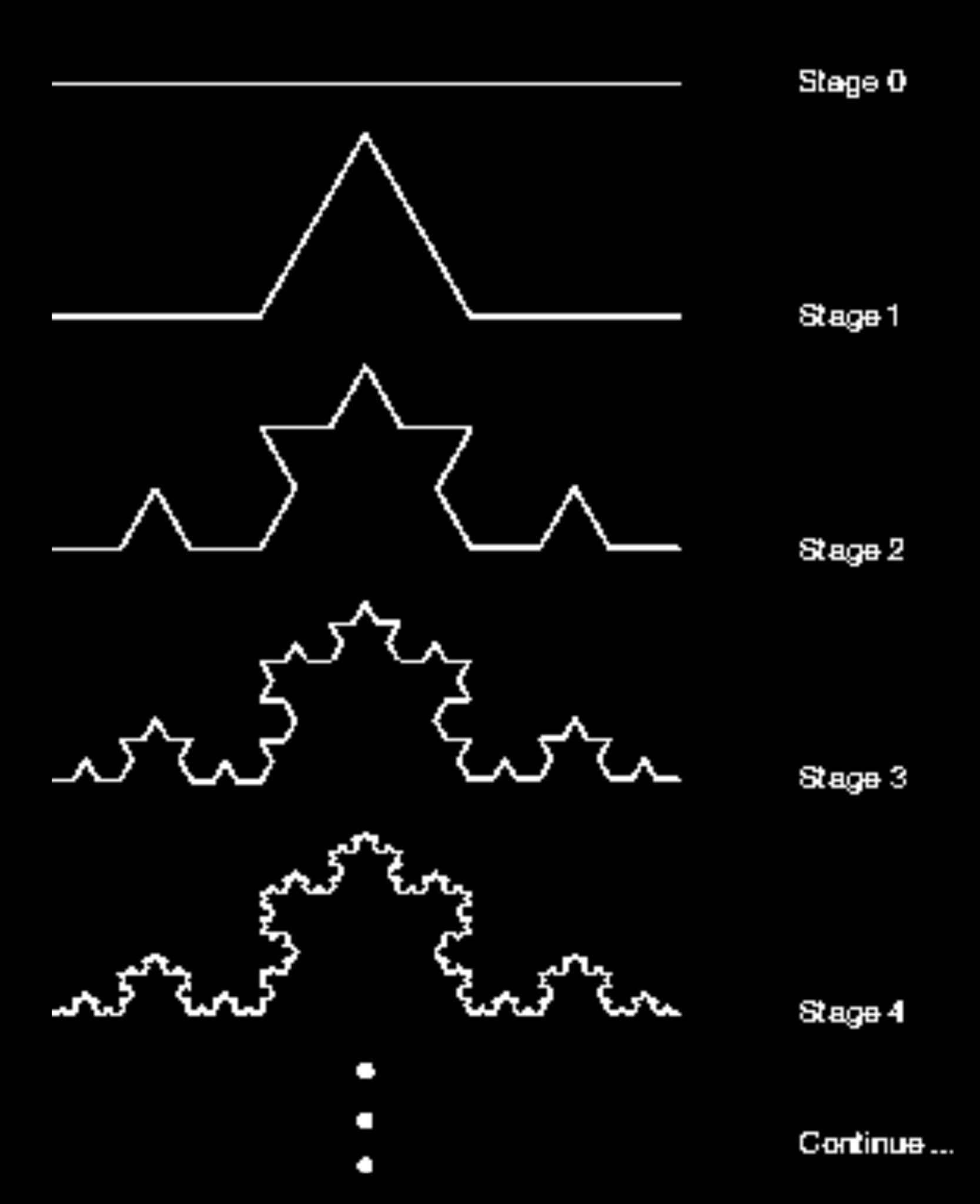
Si l'on considère ensuite le flocon de Von Koch, on s'aperçoit que le périmètre tend toujours vers l'infini, tant qu'on ajoute des segments supplémentaire, tandis que l'aire n'augmente plus en semble tendre vers une limite finie.
